BSTree Insert
Flatten
Write a function that flattens a tree, while preserving order. Flattening is the process of converting a tree to a list.
flatten (Node 5 (Node 3 (Node 2 Null Null) (Node 4 Null Null)) (Node 8 (Node 7 Null Null) (Node 10 Null Null))) = [2,3,4,5,7,8,10]
Grow
Given a list of elements than can be ordered, insert them one by one into a binary search tree. Remember that for a tree to satisfy the condition that it is a binary search tree it has to have every element smaller than the current element on the left sub-tree and every element larger than the current element on the right sub-tree.
data BSTree a = Node a (BSTree a) (BSTree a) | Null
GrowBST :: (Ord a) => [a] -> BSTree a
For example the list [5, 2, 6, 1, 3, 8] should output:
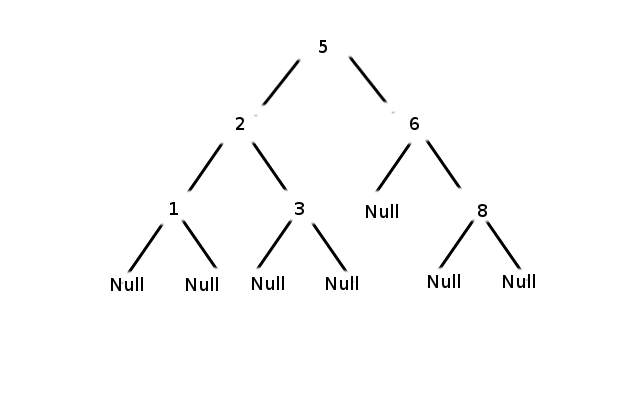
Trace your function with the input [1, 2, 3, 4] What does your tree look like? Is there a way to modify your function so that it inserts the elements in a
balanced way for a list?
Delete BST
Write a function to delete an element from a Binary Search Tree at a given index.
delete :: [a] -> Int -> [a]
Make sure you create a framework for this first – it’s tricky! You will need to find the element at the index, split the lists at this element, delete the element, and re-join the lists. If you get stuck, think about how you deleted an element from a list, and then apply this to trees.
Matrix
Matrices are mathematical objects that resembles a table. A 2x2 matrix has two rows and two columns, and four total entries. For example
| 4 | 5 |
|---|---|
| 3 | 2 |
Your first task is to create a data type for a 2x2 matrix, Matrix. Your second task is to implement a function which multiplies two matrices together. For example, the multiplication of
| a11 | a12 |
|---|---|
| a21 | a22 |
and
| b11 | b12 |
|---|---|
| b21 | b22 |
gives
| a11 b11+a12 b21 | a11 b12 + a12 b22 |
|---|---|
| a21 b11+ a22 b21 | a21 b12 + a22 b22 |
Sieve of Erasthesene
The sieve of Eratosthene is a quick way to find the first n prime numbers. It works particularly well in Haskell, which has the concept of infinite lists.
Here is what wikipedia describes the algorithm as: To find all the prime numbers less than or equal to a given integer n by Eratosthenes’ method: - Create a list of consecutive integers from 2 through n: (2, 3, 4, …, n). - Initially, let p equal 2, the smallest prime number. - Enumerate the multiples of p by counting to n from 2p in increments of p, and mark them in the list (these will be 2p, 3p, 4p, …; the p itself should not be marked). - Find the first number greater than p in the list that is not marked. If there was no such number, stop. Otherwise, let p now equal this new number (which is the next prime), and repeat from step 3. - When the algorithm terminates, the numbers remaining not marked in the list are all the primes below n.
Implement the sieve to find the first n prime numbers.
RoseTrees!
RoseTrees follow the same idea as the trees you’ve already used – you may have heard of this already! Only instead of the them being 2 leaves (binary), there can be as many branches as you want. Below is the data definition:
data Rose_Tree a = Rose_Node a [Rose_Tree a]
Write a function to map a function over all elements of the RoseTree:
mapRoseTree :: (a -> b) -> Rose_Tree a -> Rose_Tree b
Write a function to count all elements of a RoseTree:
countRose :: Rose_Tree a -> Int
Write a function to add all the elements of a RoseTree (assuming all elements are numbers):
countRose :: (Num a) => Rose_Tree a -> Int
Write a function to flatten all elements of the Rose_Tree to a list:
flattenRose :: Rose_Tree a -> [a]
Extension: How would you write this so that all elements are flattened in order?