Understanding Trees and Huffman

Understanding Huffman

Huffman is actually easier to understand backwards. Have a look at the figures below; Shown is a binary tree and therefore we can represent each path using bits: 0 to the left and 1 to the right. Since the path to every leaf is unique, there will not be any confusion between them. The Huffman Tree is also generated in a way where characters with higher frequency shall have shorter depth, so that it takes lesser bit to represent their respective path.

Huffman Decode

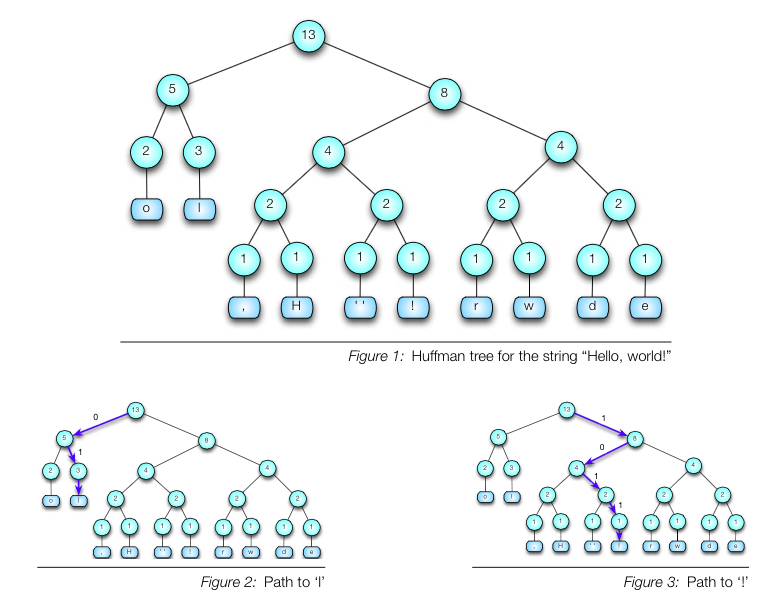
Take a look at this bit sequence:

100111110101001000101011010011000111101011

Following the tree in Figure 1, Have a go by hand decoding this bit sequence.

Discuss your observations about the tree. What was your process for decoding the bit sequence? Would it have been easier to organize the huffman encoding in a different form? (Hint: Lookup what a Lookup Table is)

Huffman Encode

This is a picture of the frequency of letters as they appear in the english language.

In groups have a go at representing this frequency in a huffman tree, draw the tree up on the white boards. Discuss why you decided to represent it that way.

Encode the sentence “The quick brown fox jumps over the lazy dog” using your huffman tree as a guide.