SuperPAL Solutions
SuperPAL
Welcome to SuperPAL questions. This worksheet is divided into 4 topics: Recursion, Higher Order Functions and Trees. At the end, there are also a few questions on Lambda Calculus and Proving Programs for COMP1130 students.
A haskell file with all solutions (except 1130 as Haskell isn’t used there) can be found here: Solution File.
Recursion
Question 1
Write a function that compresses a list by making it a list of list, where each inner list is a list of adjacent duplicates. For example:
pack [1,1,2,4,42,1,1,6,6,6,6,7,1]
= [[1,1],[2],[4],[42],[1,1],[6,6,6,6],[7],[1]]
Answer:
pack :: (Eq a) => [a] -> [[a]]
pack [] = []
pack (x:xs) = (x: (takeWhile (== x) xs)) : pack (dropWhile (== x) xs)
Question 2
Write a function that checks whether a given list of elements is increasing or not. For example:
isSorted [1,2,3,2,4,5] = False
isSorted [1,1,4,7] = True
isSorted [] = True
Answer:
isSorted :: (Ord a ) => [a] -> Bool
isSorted list = case list of
[] -> True
[x] -> True
x:y:xs -> (x <= y) && (isSorted (y:xs))
Question 3
Write a function that takes an integer and a list and drops every n’th element of that list. For example:
dropEvery [1..10] 2 = [1,3,5,7,9]
Answer:
dropEvery :: [a] -> Int -> [a]
dropEvery [] _ = []
dropEvery list count = (take (count-1) list) ++ dropEvery (drop count list) count
Question 4
A “scan” is like a cross between a map and a fold. Folding a list accumulates a single return value, whereas mapping puts each item through a function returning a separate result for each item. A scan does both: it accumulates a value like a fold, but instead of returning only a final value it returns a list of all the intermediate values. There are four different types of scans defined in the prelude namely scanl, scanr,scanl1 and scanr1.
We are going to write out own scanl. It’s type signature is:
scanl :: (a -> b -> a) -> a -> [b] -> [a]
At each step, it adds the second input to the intermediate values list, and then uses the inputted function on the second input and the first element of the list, setting the second input to the result and removing the first element from the list. At the end, it returns the list of the intermediate values. For example:
scanl (+) 2 [1..5] = 2 : (scanl (+) 3 [2..5])
= 2 : (3 : (scanl (+) 5 [3..5]))
= 2 : (3 : (5 : (scanl (+) 8 [4,5])))
= 2 : (3 : (5 : (8 : (scanl (+) 12 [5]))))
= 2 : (3 : (5 : (8 : (12 : (scanl (+) 17 [])))))
= 2 : (3 : (5 : (8 : (12 : (17 : [])))))
= [2,3,5,8,12,17]
Answer:
myScanl :: (a -> b -> a) -> a -> [b] -> [a]
myScanl f argument list = argument : (scanl f (f argument (head list)) (tail list))
Higher Order Functions
Question 1
Write a function that takes multiple sentences and removes all non-letters and capitalises all letters. For example:
onlyBigLetters "This is a short sentence. This, on the other hand, is a very very very long and drawn out sentence!"
= "THISISASHORTSENTENCETHISONTHEOTHERHANDISAVERYVERYVERYLONGANDDRAWNOUTSENTENCE"
Answer:
onlyBigLetters :: String -> String
onlyBigLetters str = map toUpper (filter isLetter str)
where
isLetter :: Char -> Bool
isLetter ch = elem ch (['a'..'z'] ++ ['A'..'Z'])
Question 2
Write a function that takes in two integers and produces a list of list that is the timetables. For example:
timetables 3 4 = [[1,2,3,4],[2,4,6,8],[3,6,9,12]]
Answer:
timetables :: Int -> Int -> [[Int]]
timetables m n = map (\x -> map (x*) [1..m]) [1..n]
Question 3
Consider the following function:
function = 0 : 1 : (zipWith (+) function (tail function))
What does this function do? What quality of haskell allows this to work?
Answer: This function produces the entire fibonacci sequence! It works because Haskell uses Lazy evaluation.
fibSeq = 0 : 1 : (zipWith (+) fibSeq (tail fibSeq))
Question 4
Give an example using booleans that shows that difference between foldl and foldr. Write out a trace for each that shows tha difference.
Answer:
list_of_booleans = [True, False, True, False]
andNot :: Bool -> Bool -> Bool
andNot a b = a && not b
foldl_function :: [Bool] -> Bool
foldl_function ls = foldl andNot True ls
-- foldl_function list_of_booleans = foldl andNot True [True, False, True, False]
-- = foldl andNot (True andNot True) [False, True, False]
-- = foldl andNot ((True andNot True) andNot False) [True, False]
-- = foldl andNot (((True andNot True) andNot False) andNot True) [False]
-- = foldl andNot ((((True andNot True) andNot False) andNot True) andNot False) []
-- = (((True andNot True) andNot False) andNot True) andNot False
-- = ((False andNot False) andNot True) andNot False
-- = (False andNot True) andNot False
-- = False andNot False
-- = False
foldr_function :: [Bool] -> Bool
foldr_function ls = foldr andNot True ls
-- foldr_function list_of_booleans = foldr andNot True [True, False, True, False]
-- = True andNot (foldr andNot True [False, True, False]
-- = True andNot (False andNot (foldr andNot True [True, False]))
-- = True andNot (False andNot (True andNot (foldr andNot True [False])))
-- = True andNot (False andNot (True andNot (False andNot (foldr andNot True []))))
-- = True andNot (False andNot (True andNot (False andNot (True))))
-- = True
Question 5
Write the reverse function using foldl.
Answer:
myReverse list = foldl (flip (:)) [] list
-- myReverse [1,2,3] = foldl (flip (:)) [] [1,2,3]
-- = foldl (flip (:)) (1:[]) [2,3]
-- = foldl (flip (:)) (2:1:[]) [3]
-- = foldl (flip (:)) (3:2:1:[]) []
-- = 3:2:1:[]
-- = [3,2,1]
Trees
Question 1
What is the difference between a binary tree, a balanced binary tree and a binary search tree? Is it possible to always have a balanced binary search tree?
Answer:
Binary trees are tree structures that always branch into two nodes. A balanced tree is simply a tree where all subtrees have equal or difference 1 depth. A binary search tree is a tree such that for all subtrees all nodes in the left-subtree are less than the root node and all nodes in the right-subtree are greater than the root node.
Provided that the tree data type has an ordering, it is always possible to create a balanced binary search tree.
Question 2
Write a function that finds the average depth of a binary tree. For example the following tree
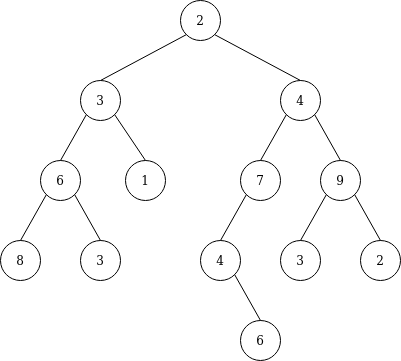
would output the following:
example_binarytree_0 = example_binarytree_0 = Node (Node (Node (Node Null 8 Null) 6 (Node Null 3 Null)) 3 (Node Null 1 Null)) 2 (Node (Node (Node Null 4 (Node Null 6 Null)) 7 Null) 4 (Node (Node Null 3 Null) 9 (Node Null 2 Null)))
averageDepth example_binarytree_0 = 4.0
Answer:
averageDepth :: BinaryTree a -> Double
averageDepth tree = fromIntegral(sum treeDepths) / fromIntegral(length treeDepths)
where
treeDepths = getDepths tree
getDepths :: BinaryTree a -> [Int]
getDepths tree = case tree of
Null -> [0]
Node l _ Null -> map (+1) (getDepths l)
Node Null _ r -> map (+1) (getDepths r)
Node l _ r -> (map (+1) (getDepths l)) ++ (map (+1) (getDepths r))
Question 3
Write a zipWith function for binary trees. For example if the zip function is +, then:
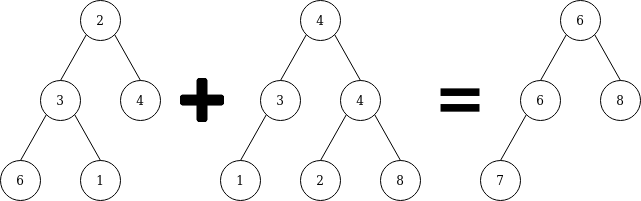
So if one tree doesn’t have the node, then the zip returns no node. In haskell, the example:
example_binarytree_1 = Node (Node (Node Null 6 Null) 3 (Node Null 1 Null)) 2 (Node Null 4 Null)
example_binarytree_2 = Node (Node (Node Null 1 Null) 3 Null) 4 (Node (Node Null 2 Null) 4 (Node Null 8 Null))
treeZipWith example_binarytree_1 example_binarytree_2 (+) = Node (Node (Node Null 7 Null) 6 Null) 6 (Node Null 8 Null)
Answer:
treeZipWith :: BinaryTree a -> BinaryTree a -> (a -> a -> a) -> BinaryTree a
treeZipWith t1 t2 f = case (t1, t2) of
(Node lt1 x rt1, Node lt2 y rt2) -> Node (treeZipWith lt1 lt2 f) (f x y) (treeZipWith rt1 rt2 f)
(Null, _) -> Null
(_, Null) -> Null
Question 4
Write a filter function for rose trees. For example, if we filtered by x `mod` 2 == 0 then:
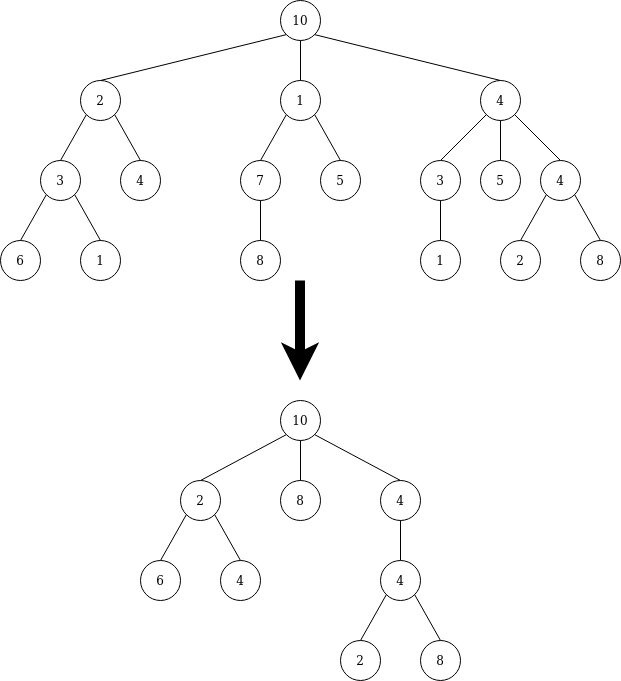
So all nodes that don’t satisfy x `mod` 2 == 0 are deleted and their children nodes moved up.
Note that if the root node doesn’t pass through the filter, than return a list of rose trees must be returned. So the type is:
treeFilter :: RoseTree a -> (a -> Bool) -> [RoseTree a]
treeFilter tree f = undefined
And the example in Haskell is:
example_rosetree = Rose 10 [Rose 2 [Rose 3 [Rose 6 [], Rose 1 []], Rose 4 []], Rose 1 [Rose 7 [ Rose 8[]], Rose 5 []], Rose 4 [Rose 3 [Rose 1 []], Rose 5 [], Rose 4 [Rose 2 [], Rose 8[]]]]
function x = (x `mod` 2) == 0
treeFilter example_rosetree function = [Rose 10 [Rose 2 [Rose 6 [],Rose 4 []],Rose 8 [],Rose 4 [Rose 4 [Rose 2 [],Rose 8 []]]]]
Hint: Write a helper function that deals with the subtrees first, i.e treeFilterHelper :: [RoseTree a] -> (a -> Bool) -> [RoseTree a].
Answer:
treeFilter :: RoseTree a -> (a -> Bool) -> [RoseTree a]
treeFilter t f = treeFilterHelper [t] f
treeFilterHelper :: [RoseTree a] -> (a -> Bool) -> [RoseTree a]
treeFilterHelper trees f = case trees of
[] -> []
(Rose x subtrees):ts -> case f x of
True -> (Rose x (treeFilterHelper subtrees f)) : treeFilterHelper ts f
False -> treeFilterHelper (subtrees ++ ts) f
COMP1130: Lambda and Proving Programs
Question 1
Which variables are bound and which variables are free in the following lambda expression?
(λz.(λy.xyw(λx.zyx)y))
Answer:
The w is free as it is not bound to any lambda. The first x is free but the second x is bound to the third lambda. All of the y’s are bound to the second lambda. The z is bound to the first lambda.
Question 2
Beta reduce the following lambda expression with both eager and lazy evaluation methods until it is in normal form.
(λz.λy.xyz) x ((λx.xx) w)
Answer:
Eager Evaluation:
(λz.λy.xyz) x ((λx.xx) w) →β (λy.xyx) ((λx.xx) w) →β (λy.xyx) (ww) →β xwwx
Lazy Evaluation:
(λz.λy.xyz) x ((λx.xx) w) →β (λy.xyx) ((λx.xx) w) →β x((λx.xx) w)x →β xwwx
Question 3
Consider the following Haskell functions:
reverse :: [a] -> [a]
reverse [] = [] --(reverse.1)
reverse (z:zs) = (reverse zs) ++ [z] --(reverse.2)
(++) :: [a] -> [a] -> [a]
(++) [] ys = ys --(++.1)
(++) (x:xs) ys = x : (xs ++ ys) --(++.2)
sum :: [a] -> [a]
sum [] = 0 --(sum.1)
sum x:xs = x + (sum xs) --(sum.2)
Prove that sum (reverse ls) = sum ls
Hint: You may want to first prove the Lemma: sum (xs ++ ys) = (sum xs) + (sum ys).
Answer:
We will first prove the Lemma sum (xs ++ ys) = (sum xs) + (sum ys) by induction on the length of xs.
Base case: Suppose xs is [], then
sum ([] ++ ys)
= sum (ys) --(By ++.1)
Induction step: Our induction hypothesis is sum (zs ++ ys) = (sum zs) + (sum ys) and we must show that the statement then holds for sum (z:zs ++ ys) = (sum z:zs) + (sum ys)
sum (z:zs ++ ys)
= sum (z : (zs ++ ys)) --(By ++.2)
= z + sum (zs ++ ys) --(By sum.2)
= z + (sum zs) + (sum ys) --(By Induction hypothesis)
= sum (z:zs) + (sum ys) --(By sum.2)
We will now prove the original statement sum (reverse l) = sum (l) by induction on the length of ls
Base case: Suppose ls is [], then
sum (reverse [])
= sum ([]) --(By reverse.1)
Induction step: Our induction hypothesis is sum (reverse xs) = sum (xs) and we must show that the statement then holds for sum (reverse x:xs) = sum (x:xs)
sum (reverse (x:xs))
= sum (reverse (xs) ++ [x]) --(By reverse.2)
= sum (reverse xs) + sum ([x]) --(By Lemma)
= (sum xs) + sum ([x]) --(By Induction hypothesis)
= (sum xs) + sum (x:[]) --([x] is syntactic sugar for x:[])
= (sum xs) + x + sum([]) --(By sum.2)
= (sum xs) + x + 0 --(By sum.1)
= (sum xs) + x --(0 is additive identity)
= x + (sum xs) --(Commutativity of +)
= sum (x:xs) --(sum.2)