Trees Solutions

Question: Draw Your Own Trees

Below we have written out two instances of Binary Trees. Draw each one:

1. Node (Node Null -5 Null) 10 (Node Null 7 Null)
2. Node (Node (Node Null 'a' Null) 'b' (Node Null 'c' Null)) 'd' (Node (Node Null 'e' Null) 'f' Null)

Answers:

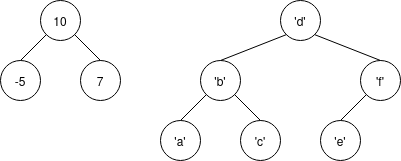
Now we have drawn some example trees. Convert them to Haskell and write their type:

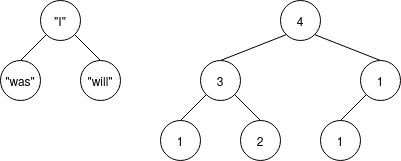
Answers:

1. Node (Node Null "was" Null) "I" (Node Null "will" Null). Type: BinaryTree String.
2. Node (Node (Node Null 1 Null) 3 (Node Null 2 Null)) 4 (Node (Node Null 1 Null) 1 Null). Type: BinaryTree Int.

Question: Binary Tree Functions

1. Write a function treeNodes that counts the total number of nodes in a binaryTree. For example:

treeNodes (Node (Node (Node Null 1 Null) 2 Null) 3 (Node (Node (Node Null 4 Null) 5 Null) 6 (Node (Node Null 7 Null) 8 (Node (Node Null 9 (Node Null 10 Null)) 11 (Null))))) = 11

Answer:

treeNodes :: BinaryTree a -> Int
treeNodes tree = case tree of
    Null                            -> 0
    Node (leftTree) _ (rightTree)   -> 1 + (treeNodes leftTree) + (treeNodes rightTree)

1. Write a function to calculate the depth of a tree. (See above for definition and example). For example:

treeDepth (Node (Node (Node Null 1 Null) 2 Null) 3 (Node (Node (Node Null 4 Null) 5 Null) 6 (Node (Node Null 7 Null) 8 (Node (Node Null 9 (Node Null 10 Null)) 11 (Null))))) = 6

Answer:

treeDepth :: BinaryTree a -> Int
treeDepth tree = case tree of
    Null                            -> 0
    Node (leftTree) _ (rightTree)   -> 1 + (max (treeDepth leftTree) (treeDepth rightTree))

1. Write a treeMap function that maps a function to all the values inside a tree. For example:

treeMap (+1) (Node (Node (Node Null 1 Null) 2 Null) 3 (Node (Node (Node Null 4 Null) 5 Null) 6 (Node (Node Null 7 Null) 8 (Node (Node Null 9 (Node Null 10 Null)) 11 (Null)))))
= Node (Node (Node Null 2 Null) 3 Null) 4 (Node (Node (Node Null 5 Null) 6 Null) 7 (Node (Node Null 8 Null) 9 (Node (Node Null 10 (Node Null 11 Null)) 12 Null)))

Answer:

treeMap :: (a-> b ) -> BinaryTree a -> BinaryTree b
treeMap f tree = case tree of
    Null                            -> Null
    Node (leftTree) a (rightTree)   ->  Node (treeMap f leftTree) (f a) (treeMap f rightTree)

Question: Draw Rose Trees

1. Now that you understand what a rose tree is, draw the rose tree corresponding to the following code representation:

Rose 15 [Rose 3 [], Rose 5 [Rose 1 [], Rose 3 [], Rose 7 []]]

Answer:

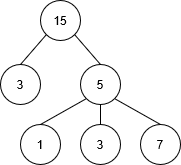
1. Now write out the haskell code that would correspond to the following rose tree:

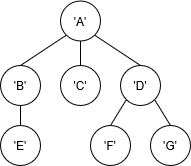
Answer:

Rose 'A' [Rose 'B' [Rose 'E' []], Rose 'C' [], Rose 'D' [Rose 'F' [], Rose 'G' []]

Question: Rose Tree Functions

Implementing functions that operate on rose trees is very similar to Binary trees, however, instead of recursing to the left child and right child, you will need to iterate through the entire list of children. With this in mind, implement the Binary tree functions you implemented earlier for Rose trees.

1. Implement roseTreeNumNodes which takes a rose tree and returns the number of nodes.

Answer:

data Rose a = Rose a [Rose a]
    deriving (Show)

roseTreeNumNodes :: (Rose a) -> Integer
roseTreeNumNodes (Rose a children) = 1 + sum (map roseTreeNumNodes children)

1. Implement roseTreeHeight which takes a rose tree and returns the height.

Answer:

data Rose a = Rose a [Rose a]
    deriving (Show)

roseTreeHeight :: (Rose a) -> Integer
roseTreeHeight (Rose a children) = 1 + foldl max (0) (map roseTreeHeight children)

1. Implement roseTreeMap which takes a function and a rose tree and recursively applies that function to every element of the rose tree.

Answer:

data Rose a = Rose a [Rose a]
    deriving (Show)

roseTreeMap :: (a -> b) -> (Rose a) -> Rose b
roseTreeMap f (Rose x children) = Rose (f x) (map (roseTreeMap f) children)