Higher Order Functions and Lists
Revision: List Recursion
By now you have seen recursion on lists many times, but just in case, let’s have a quick recap!
Writing recursive functions on lists requires you to understand what List structure and Recursion are:
-
Lists are powerful data structure for storing a sequence of elements, all of the same type,
a. They are defined recursively, as either the empty list[]or an element attached to the front of another lista : [a]. -
The essential structure of recursion is:
- Base Case: the terminal output on the simplest case..
- Recursive Case: the looping output which which is what we keep call the function itself for your desired operation.
Basically, when you write functions on lists, you uses recursive definitions that traverse the list structure.
For example, for a recursive function which counts the length of an input list, we start from considering the case which input list is empty:
length [] = 0
And then we must consider the step case where the list has the form a : [a]:
length (x:xs) = 1 + length xs
Putting them together:
length :: [a] -> Int
length [] = 0 -- base case
length (x:xs) = 1 + length xs -- step case
That is basically it! Doing recursion on lists simply involves breaking it down into the two steps, one for each of the list definitions, [] and a : [a]!
Question: Writing List Recursion Functions
Here are some questions to help you revise list recursion. Note that the Answers are just one of many possible implementations.
-
Implement the function
addOne :: [Int] -> [Int]which takes a list and adds one to each element. E.gaddOne [1, 2] = [2, 3]. -
Implement the function
multiplyN :: Int -> [Int] -> [Int]which takes a list and multiplies each element by a constant somultiplyN 3 [1, 2] = [3, 6]. -
Implement the function
addList :: (Num a) => [a] -> [a] -> [a]which takes two lists and adds each element to the corresponding element in the other list, soaddList [3, 5] [1, 2] = [4, 7]. Note thataddListshould produce an error if the lists have different lengths. -
Implement the function
removeNegative :: [Int] -> [Int]which takes a list and removes all the negative elements, soaddList [1, -2, 3, -4] = [1, 3].
Higher Order Functions
By now, you should be very familiar with the standard haskell syntax:
hello :: String -> String -- type signature
hello name = "Hello, " ++ name ++ "!" -- function definition
We have also seen a variety of different type signatures:
tup :: (a,b) -> a -- tuples
multiInput :: a -> b -> c -- multiple inputs
lists :: [a] -> [a] -- lists
types :: Maybe a -> Maybe b -- interesting and cool types
So, really as long as the type exists by itself, then we can put it in as an input or output for a function!
Given this, consider the following functions:
fst :: (a,a) -> a
fst (x,_) = x
snd :: (a,a) -> a
snd (_,y) = y
These are clearly valid functions with valid types. So we can use these types as normal input and outputs, right?
tup1or2 :: Int -> ((a,a) -> a)
tup1or2 i = case i of
1 -> fst
2 -> snd
_ -> error "Tuple only has two elements"
What we have made here is a **Higher Order** function: it is a function that acts on other functions! For tup1or2 specifically, the function takes in a integer and returns the functions fst or snd for 1 and 2 respectively! Let’s see it in action:
tup1or2 1 = fst :: (a,a) -> a
tup1or2 2 = snd :: (a,a) -> a
tup1or2 3 = error "Tuple only has two elements"
Given that it outputs a function, we can then immediately apply its output to a tuple:
(tup1or2 1) ('a','b') = fst ('a', 'b')
= 'a'
(tup1or2 2) ('x','y') = snd ('x', 'y')
= 'y'
So, as we saw with all other types, we can use functions in types signatures as we wish! Let’s look at an example that uses a function as the input:
applyTup :: (a -> b) -> (a,a) -> (b,b)
applyTup f (x,y) = (f x, f y)
So this applyTup function takes a function and a tuple and then applies the input function to each of the values in the tuple. This is all well defined, as the types all align and match. Here some examples of it in action:
applyTup (+2) (-1,1) = (1,3)
applyTup toUpperCase ('a', 'b') = ('A', 'B')
So functions are just like any other type in haskell, giving us the ability to use use them as we wish. Here are some other higher order functions:
which :: Bool -> (a -> b) -> (a -> b) -> a -> b
which b f1 f2 x = case b of
True -> f1 x
_ -> f2 x
applyIteratively :: Int -> (a -> a) -> a -> a
applyIteratively i f x
| i > 1 = f (applyIteratively (i-1) f x)
| i == 1 = f x
| otherwise = error "Must apply a positive number of times"
-- Here we use a lambda expression to define the output!
power :: (Floating a) => a -> (a -> a)
power n = (\x -> x ** n)
Questions: Type Signatures for Higher Order Functions
Below, we have a variety of function definitions. All of these define higher order functions. For each, add the type signature. Remember to use polymorphism to make them as general as possible!
apply :: ____________
apply f x = f x
curry :: ____________
curry f x y = f (x,y)
multiplyTwice :: ____________
multiplyTwice n = (\x -> x * n * n)
The curry function is quite difficult: feel free to look it up if you are having trouble. As it turns out, it forms the basis of many haskell operations!
Questions: Type Signatures to Function Definition
Now we have the opposite: a lot of type signatures but no function definitions! Fill in the blanks and define the functions below based on their names, inputs and type signatures:
add :: Int -> (Int -> Int)
add n = ____________
choose :: Int -> [a -> b] -> a -> b
choose i listOfFunctions x = ____________
Remember the function: (!!) :: [a] -> Int -> a.
Questions: Your Own Higher Order Function
Write the type signature for and define a higher order function that does the following: takes in two functions and a tuple and then applies the first function to the left tuple value and the second function to the right tuple value. This will return a tuple. For example:
func (+1) toUpper (0, 'i') = (1, I)
Higher Order Functions on Lists
In this course, a lot of time is spent manipulating lists in one way or another, and higher order functions are an especially useful way of dealing with data structures such as lists. Due to this, there are many predefined Prelude higher order functions that work on lists.
The most basic example of this is filter: it simply takes an input Boolean function which checks for some condition on each element of the list and an input list, and then returns the list of all the elements which satisfied the condition. For example:
filter :: (a -> Bool) -> [a] -> [a]
filter odd [1,2,3,4,5,6] = [1,3,5]
filter even [1,2,3,4,5,6] = [2,4,6]
Of course you aren’t limited to only prelude functions as inputs for higher order functions, you can define your own:
isSmall :: Int -> Bool
isSmall num
| num < 10 = True
| otherwise = False
filter isSmall [8,9,10,11,12] = [8,9]
map is a higher order function which applies a function to every element of a list and then puts this output back into the list. Here is a fun example using reverse:
map :: (a -> b) -> [a] -> [b]
map reverse ["abc", "123", "xyz"] = ["cba", "321", "zyx"]
Note here how even though each string element has been reversed, the whole list itself is still in the same order.
zipWith is another higher order list Prelude function. This function takes as inputs two lists of the same length, and a function which takes two inputs. Each pair of elements at the same index in each list is fed into the function, and then the list is built from each output:
zipWith :: (a -> b -> c) -> [a] -> [b] -> [c]
zipWith (*) [5,6,7] [3,4,5] = [15,24,35]
Finally, we have the folding higher order functions: foldl and foldr. These functions take a two input function, a list, and an accumulator as arguments. Then they apply the function to the accumulator and the first element of the list to generate a new accumulator. This is done iteratively until the entire list has been ‘folded’ through, giving one final output.
In other words: to calculate the result of the fold functions, the input function will be first applied to the first element of the list and the starting value of the accumulator. The list is then parsed through, with each application of the function being applied to the next element and the accumulator, so that the list is combined or ‘folded’ into one result.
The difference between foldl and foldr is shown in this diagram:
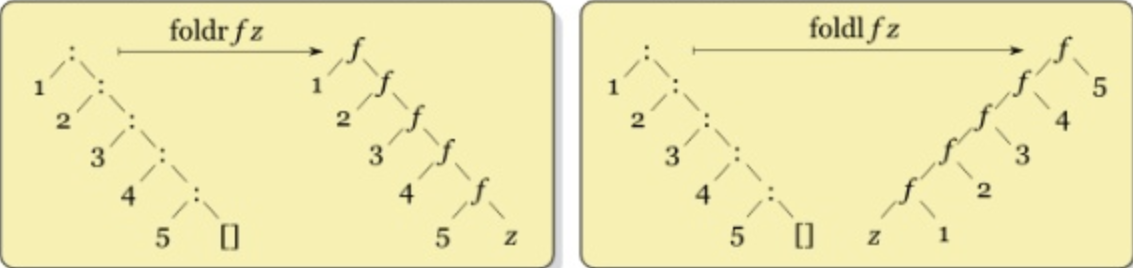
In the example below, the input function is +, the accumulator is 0. So the first step is to add 0 and 1. This result will then become the new accumulator for the next step of the function. This new accumulator is then combined with the second element, and so on.
foldl :: (a -> b -> a) -> a -> [b] -> a
foldl (+) 0 [1,2,3,4,5] = 15
Here is another example where foldr and foldl give different results as they start at different sides of the list:
foldl (/) 10 [2,5,10] = foldl (/) 5 [5,10]
= foldl (/) 1 [10]
= foldl (/) 1/10 []
= 1/10
foldr (/) 10 [2,5,10] = foldr (/) 1 [2,5]
= foldr (/) 5 [2]
= foldr (/) 2/5 []
= 2/5
Questions: Writing Higher Order Functions on Lists
Now that you have some familiarity with higher order functions which operate on lists, have a go at writing your own version of the functions! Do this for map, zipWith, foldl and foldr.