Complexity

Complexity Revision

Luckily for you, complexity is one of the least complex topics in COMP1100. Colloquially, complexity is just a measure of how many resources a program takes up, and is a measure of efficiency. Efficiency can be measured in many ways - in terms of time (CPU time), memory, or network usage among others.

Here, we mainly focus on time complexity: What happens as the size of the problem being solved gets larger?

The time required by a function/procedure is proportional to the number of “basic operations” that it performs. e.g. reading over a single element in a list. Some functions/procedures perform the same number of operations every time they are called, while other functions may have a different number of operations depending on the input, or by chance.

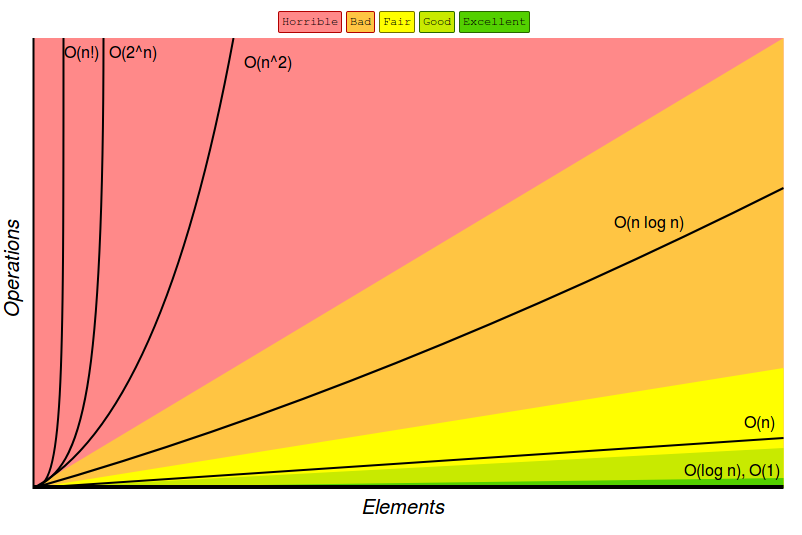
Complexity is typically represents as a rate of growth proportional to the input size n with big-O notation. Here are several classes of functions that are commonly encountered while analysing the complexity of functions:

Big-O Notation	Name
O(1)	constant
O(log(n))	logarithmic
O(n)	linear
O(nlog(n))	linearithmic
O(n^2)	quadrative
O(n^c)	polynomial
O(c^n)	exponential

where c is a constant

Typically, we are usually interested in the worst case: what is the maximum number of operations that might be performed for a given problem size. This is what is typically represented by O(n). For practical purposes, we are also interested in the average case: represented by Θ(n).

Here is a useful visualisation for complexity:

Problems

Time to have a go yourself! And please don’t be afraid to ask for help. That’s what the whole study event is for.

Adding an element to a list

Write a function to add an element to a list. Note that there are mutiple ways to do this, and the complexity may change accordingly.

What is the time complexity of the function you have written?

Reverse (++)

We have written the following function:

reverse :: [a] -> [a]
reverse list = case list of
  [] -> []
  x:xs -> (reverse xs) ++ [x]

Find the complexity of the reverse function above. Is there a better way to implement this? What would be the lowest complexity for the reverse function?

Minimum length list

We have written the following function:

  short :: [[a]] -> Int
  short ls = helper ls 0
    where
      helper :: [[a]] -> Int -> Int
      helper rows idx = case rows of
        []   -> helper ls (idx + 1)
        l:ls -> case (l !! idx) of
            [] -> idx
            _  -> helper ls idx

Find the complexity of the short function above. Note: assume there are c lists in the list of lists.

Cannibals and Missionaries

Consider the classic problem of cannibals and missionaries. The problem goes as follows: There are 3 cannibals and 3 missionaries, stuck on one side of a river with a bout. The aim is to get all of them to the other side of the river. The boat can only carry two and requires one to operate it. One of the cannibals cannot operate it because he has lost an arm…somehow. If the cannibals outnumber missionaries at any point, then the cannibals will eat the missionaries.

Find the shortest way for everyone to get across the river without anyone being eaten. What was the complexity of the function you used to find the answer?

Note: Implementation always shows deeper understanding, but a conceptual answer for this question is fine too

Sorts

Hopefully you have gained a good understanding of complexity. One of its main applications is in sorting: we always want to sort in the minimum time possible.

Mergesort

Conceptually, mergesort works as follows:

1. Divide the unsorted list by halving the list until there are n sublists of 1 element (an element of 1 is considered sorted)
2. Repeatedly merge sublists to produce new sorted sublists until there is only 1 sublist remaining. This will be the sorted list.

Here’s an example of how it works:

Implement the mergesort algorithm in Haskell, if you can. Using this function or otherwise, determine the complexity of the algorithm.

Quicksort

Conceptually, quicksort works as follows:

1. Pick the first element of the list as a “pivot”
2. Reorder the array so that all elements with values less than the pivot come before the pivot, while all elements with values greater than the pivot come after it (equal values can go either way). After this partitioning, the pivot is in its final position. This is called the partition operation.
3. Recursively apply the above steps to the sub-array of elements with smaller values and separately to the sub-array of elements with greater values.

Here’s an example of how it works:

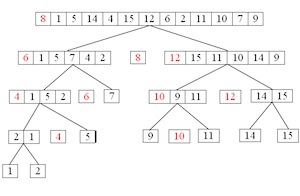
Implement the quicksort algorithm in Haskell, if you can. Using this function or otherwise, determine the complexity of the algorithm. Is there a better way to implement this? What are the average and worst case complexities for the quicksort function?

Hint: Use list comprehensions!

Challenge Question: Bogosort

This one’s an interesting one. Don’t worry if you don’t recognise all the code in here, focus on the conceptual details. Before you do anything, what does this program actually do?

-- http://rosettacode.org/wiki/Sorting_algorithms/Bogosort#Haskell
import System.Random
import Data.Array.IO
import Control.Monad
isSorted :: (Ord a) => [a] -> Bool
isSorted (e1:e2:r) = e1 <= e2 && isSorted (e2:r)
isSorted _ = True

-- from http://www.haskell.org/haskellwiki/Random_shuffle
-- TL;DR it randomly shuffles the list
shuffle :: [a] -> IO [a] -- This is what requires all the imports
shuffle xs = do
        ar <- newArray n xs
        forM [1..n] $ \i -> do
        j <- randomRIO (i,n)
        vi <- readArray ar i
        vj <- readArray ar j
        writeArray ar j vi
        return vj
  where
    n = length xs
    newArray :: Int -> [a] -> IO (IOArray Int a)
    newArray n xs = newListArray (1,n) xs
    
-- This new ">>=" symbol can be thought of as simply "stripping"
-- the IO type from the output of shuffle, i.e. making it type [a]
bogosort :: (Ord a) => [a] -> IO [a]
bogosort li | isSorted li = return li
| otherwise = shuffle li >>= bogosort

What are the average and worst time complexities of this program? Hint: Does bogosort ever terminate?