PAL Plays Tic-Tac-Toe
Overview
Over the past 10 weeks, you have learnt a lot of different concepts in computer science and how to implement these in Haskell. Putting all these different concepts together, we can make a bot that plays Tic-Tac-Toe!
Instead of immediately leaping into building a bot, let’s break down the steps that are reqiured: 1) Heuristics: We need our bot to be smart and evalute the game states intelligently. To do so, we need to develop a set of heuristics that accurately guess how good a position will be. 2) Game Tree: Last week in PAL we learned how to build a game tree and make a move using a greedy bot, so we can assume that you already know how to build your own game tree (If you get stuck, take a look back at last week’s worksheet) 3) Minimax: With our game tree, we can use minimax to evalute what the best possible future position will be. We can then make a bot that will select the move that will lead to that future game state.
Background
Last week, we worked to make a greedy bot in Tic-Tac-Toe. This resulted in the following data types and functions:
data Board = [Move]
data Move = (Player, (Int, Int)) -- X, Y coordinates
data Player = X | O
deriving (Show, Eq)
-- Returns a number on how good a board is, bigger is better
evaluateBoard :: Board -> Int
-- Assuming the move is valid, make the move and returns the new board
makeNextMove :: Board -> Move -> Board
-- Returns true if a move is able to be made in this board
isValidMove :: Board -> Move -> Boolean
-- Returns the move that will result in the best next board
greedyMove :: Board -> Player -> Move
-- Gets all the possible moves that a player can do ever
allMoves :: Player -> [Move]
-- Gets all the valid moves that a player can do with the current board
validMoves :: Board -> [Move] -> [Move]
-- Scores a list of moves with the evaluateBoard function
scoreMove :: Board -> [Move] -> [(Int, Move)]
-- Returns the best move from a list of moves and their scores
maximum' :: [(Int, Move)] -> Move
We call these types of function the Backend: it runs the game in the background so that we can interact with it.
Heuristics
So what is a heuristic? Well suppose we have a game state and we want to know how well Player 1 is doing in this game state: the heuristic evaluates this game state and outputs a score. The higher the score, the better Player 1 is doing.
Eventually we will use heuristics to evaluate the leaf nodes in minimax. This will make the bot choose the moves that will lead to game states that is is more likely to win from. But at the moment, you can just imagine applying the heuristics to a greedy bot: what move should I make NOW.
What are some heuristics? How does someone make one? Well let’s look at some examples. Here we use the game chess as our game:
- How many pieces Player 1 has on the board?
- What is the difference of in the total scores of the pieces between Player 1 and Player 2?
- How many “good” pieces does Player 1 have left?
- How many possible moves can Player 1 make (i.e how open is their position)?
Now it is your turn! Try come up with some heuristics for tic tac toe. Once you have a 2 or so, choose two and write them in Haskell: basically, implement 2 or so version of the evaluateBoard :: Board -> Int.
Minimax
Now that you have several heuristics to use and a game tree, we can get started on minimax!
Minimax is an algorithm that you can use to evaluate the best possible move to make for a given game tree. The algorithm relies on using some heuristic function to evaluate the end board states (the leaf nodes of the game tree), and passing these values up the tree to find the best move. As an example, take this simple tree:
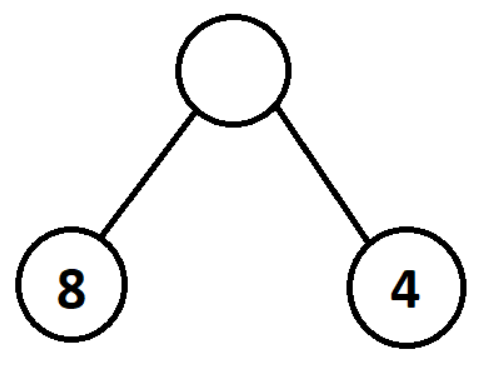
If we are wishing to maximise the score for the root node, then we compare the values of all the children, and choose the maximum to “pass” up to the parent node.
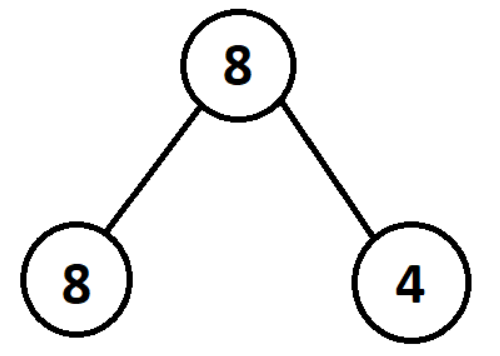
The parent node now contains the value of the best result of its children. This process is then repeated for all nodes, alternating beetween maximising and minimising at each level, until the entire tree has been completed. We alternate between maximising and minimising to represent the alternative turns between you and your opponent: your opponent is going to choose your worst game state!
1) Using a diagram, perform a Minimax algorithm on these balanced binary search trees with the following terminal node pairs:
(-2, 4) (15, 0) (3, 11) (-7,-9)
2) Create a Minimax function with a lookahead value of 1 (look one turn into the future). 3) Write a general Minimax function that works for a certain depth:
minimax :: RoseTree a -> Int -> a
minimax tree depth = # RETURN BEST LEAF NODE #