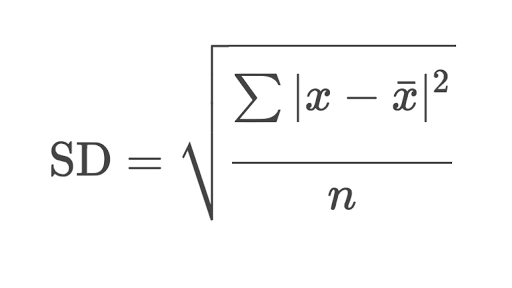Week 8

A very useful skill to have in any programming problem is the ability to break down a problem and solve it from the bottom up. As you learn more functions and data types, the kinds of problems you will be faced with become more and more complicated, which means that trying to write one big function which does everything becomes nearly impossible. In today’s session, we will be writing a function which calculates the standard deviation of an arbitrary list of numbers. The formula for standard devaition is as follows:

std_dev

You could try can create a function that calculated the standard deviation in one go but I bet you it would take a long time do to and take even longer to debug! If you look closely you can see that the standard deviation is the composition of many functions. Square root, summation, squaring, division…All of these operations are technically their own function and should be treated as such when the probem is decomposed and functionally recomposed together.

Standard deviation is an averaged measure of each individual element’s distance from the mean of the set. As such, the first step should be to write a function to calculate the mean of the set. Bear in mind that there are often many helpful prelude functions that you can use to make your job easier; can you think of one which could help to find the mean?

mean :: [Double] -> Double

After we have the mean, we can calculate the squared difference between each element and the mean:

squareDiff:: Double -> Double 

With all of that complete, we can now combine these to find the Standard Deviation:

standardDev :: [Double] -> Double

Take it from the top

Using the definition below calculate the normal probablity density function for a distribution and a value in the distribution. For this problem we will not be providing definitions for helper functions, but you are advised to use where clauses to assist with your solution.